Simulation¶
In addition to decoding protocols, Ripyl provides functions for simulating realistic waveforms. All of the protocols come with a synthesis function that generates edge streams. Such streams can be fed into the corresponding decoder to retrieve the original data. These edge streams can be further enhanced by converting them to sample streams and applying transformations that replicate real world effects such as noise and band-limited edges. This capability is used in Ripyl’s own test suite to generate arbitrary randomized test data for validating the decoders.
Signal Processing¶
The sigproc module provides a number of functions for transforming sampled data. The following examples process a set of samples created from a short edge stream describing a pulse:
import ripyl
import ripyl.sigproc as sigp
pulse_edges = [(0.0, 0), (1.0, 1), (3.0, 0), (4.0, 0)]
sample_rate = 100.0 # Sample at 100Hz
sample_period = 1.0 / sample_rate
pulse_samples = list(sigp.edges_to_sample_stream(iter(pulse_edges), sample_period))
# NOTE: pulse_samples is a list of SampleChunk objects rather than raw samples
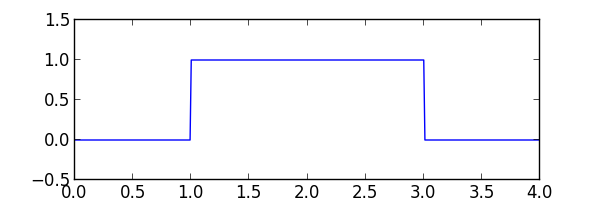
Amplify¶
The amplify() function is used to apply a gain and offset to a waveform.
proc_samples = sigp.amplify(iter(pulse_samples), gain=0.5, offset=1.1)
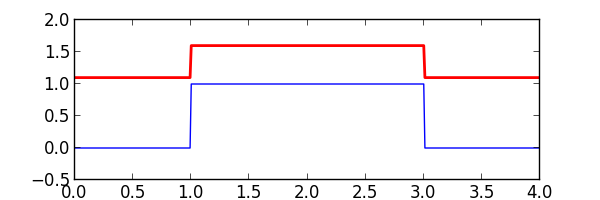
Invert¶
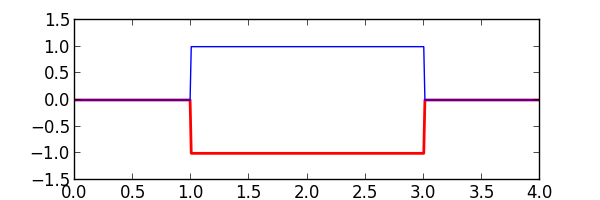
The invert() function is used to invert the polarity of a waveform. It is the equivalent of amplify(..., gain=-1.0)
proc_samples = sigp.invert(iter(pulse_samples))
Dropout¶
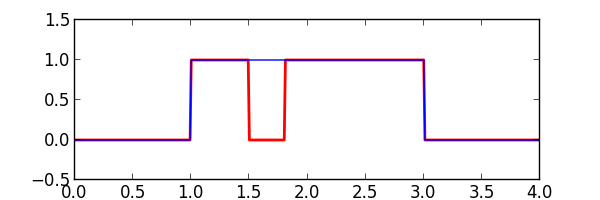
The dropout() function is used to simulate the corruption of a waveform by forcing samples to a fixed level for a span of time. This provides a convenient way to inject errors into a sample stream for testing a decoder’s error handling.
# Force samples to the default 0.0V.
proc_samples = sigp.dropout(iter(pulse_samples), start_time=1.5, end_time=1.8)
Noisify¶
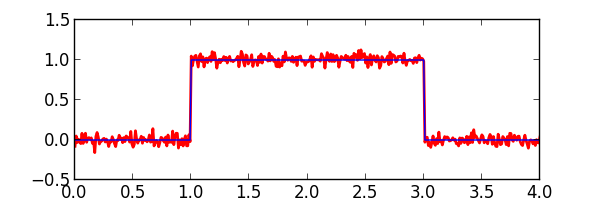
The noisify() function adds arbitrary levels of gaussian noise to a waveform. It takes an SNR level in the form of a positive valued number. This value is only accurate if the input samples are normalized to the range 0.0 to 1.0. Any amplification should be applied after noisify() for the SNR to be correct. An SNR over 80 will bypass the noise generation process and just pass the original samples through.
proc_samples = sigp.noisify(iter(pulse_samples), snr_db=20.0)
Quantize¶
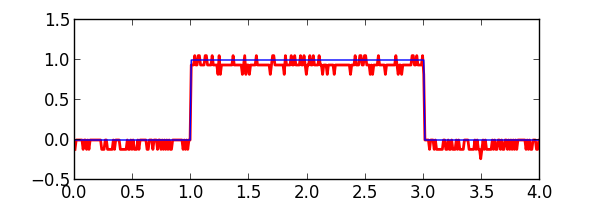
The quantize() function simulates the effect of ADC sample quantization by restricting samples to discrete levels. It is best visualized when used in conjunction with noisify(). The full_scale parameter specifies the voltage range of the ADC. Along with the specified number of ADC bits (default is 8) the discrete levels are separated by \(\text{full_scale} / 2^{bits}\) volts. The output will not be clipped if the input levels extend beyond the range of full_scale. When this happens the effective number of bits is greater than what is specified with the bits parameter.
# The input pulse spans 0.0V to 1.0V (before noise). A 30V range means that an 8-bit ADC
# will quantize to 30.0 / 2**8 = 117mV steps.
proc_samples = sigp.quantize(sigp.noisify(iter(pulse_samples), snr_db=20.0), full_scale=30.0)
Filter waveform¶
The filter_waveform() function performs a low-pass FFT on a sample stream. The filter parameters are specified with a sample_rate and a rise_time parameter that sets the approximate edge rate for the rising and falling edges. A Kaiser window function is used to generate filter coefficients. The min_rise_time() helper function provides the minimum rise time value for a given sample rate for a system with gaussian response (\(\text{rise_time} \approx 0.35 / BW\)).
rt = sigp.min_rise_time(sample_rate) * 20.0
proc_samples = sigp.filter_waveform(iter(pulse_samples), sample_rate=sample_rate, rise_time=rt)
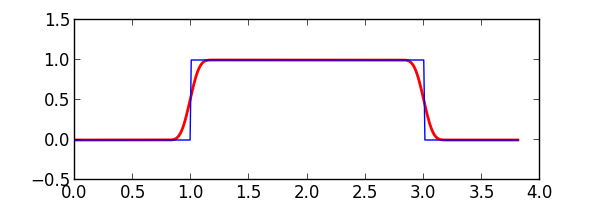
Capacify¶
The capacify() function simulates a first-order RC filter applied to a sample stream. The result is rising and falling edges that exhibit exponential decay. This function iteratively computes the capacitor voltage to simulate the filter output for each sample. The default number of iterations is 80. If the iterations is set too low the output can exhibit erroneous artifacts due to numeric instabilities. This is dependent on the input waveform sample values, the sample period, and the time constant. There is a native Python implementation and a Cython implementation of this function. The native implementation is prohibitively slow if more than about 5 iterations is performed. If Cython is unavailable it is important to be careful when the iterations are reduced.
We establish an initial capacitor voltage and charge from the first sample \(v_c = v_{sample}(0); q_0 = v_c * c\). For each iteration of the simulation we increment time such that \(dt = \text{sample_period} / \text{iterations}\):
tau = 0.25
r = 1.0
c = tau / r # Still 0.25 in this case with 1.0 Ohm of resistance
proc_samples = sigp.capacify(iter(pulse_samples), capacitance=c, resistance=r)
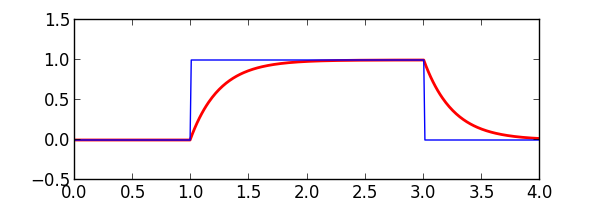
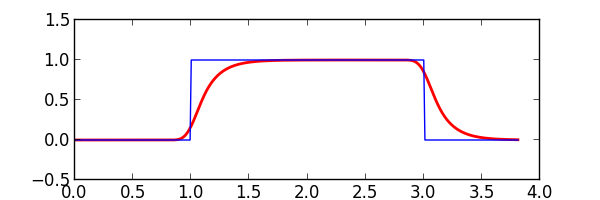
synth_wave¶
The synth_wave() function is a wrapper around edges_to_sample_stream(), capacify(), and filter_waveform(). It provides an easy way to directly convert an edge stream into a realistic sampled waveform with band-limited edges. The capacify() parameters are specified indirectly using the tau_factor parameter. This establishes the magnitude time constant tau in relation to the rise time. The capacify() operation is bypassed if the tau_factor is below 0.01
rt = sigp.min_rise_time(sample_rate) * 20.0
proc_samples = sigp.synth_wave(iter(pulse_edges), sample_rate=sample_rate, \
rise_time=rt, tau_factor=1.0)
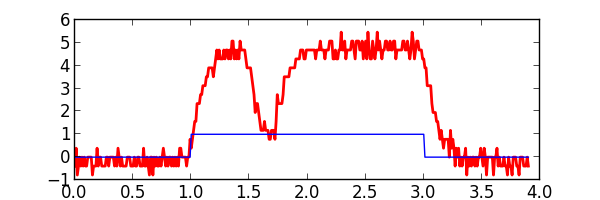
Combining operations¶
The signal processing operations can be combined together in sequence to perform more complex processing of sampled waveforms.
rt = sigp.min_rise_time(sample_rate) * 10.0
tau = rt * 1.5
r = 1.0
c = tau / r
proc_samples = sigp.dropout(iter(pulse_samples), start_time=1.5, end_time=1.7)
proc_samples = sigp.filter_waveform(sigp.capacify(proc_samples, c, r), \
sample_rate=sample_rate, rise_time=rt)
proc_samples = sigp.quantize(sigp.noisify(proc_samples, snr_db=20.0), full_scale=20.0)
proc_samples = sigp.amplify(proc_samples, gain=5.0)